表面積の公式 141969-表面積���公式 球
3
この円柱の側面積= 球の表面積の公式と同じ式をしていることが分かる. あなたは今、球の表面積を求める公式を知らないものとします. 円柱の側面積=球の表面積 を示すことによって, (円柱の側面積= なので,) 球体の表面積= を示すことができます. 輪切りの考え方 円柱と球を真円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学 > 図形 > 円錐台の体積と表面積を計算する公式と証明 最終更新日 図のような円錐台について、 体積は、 V = 1 3 π h ( a 2 a b b 2) 側面積は、 S L = π ( a b) ( a − b) 2 h 2 表面積は、 S
表面積の公式 球
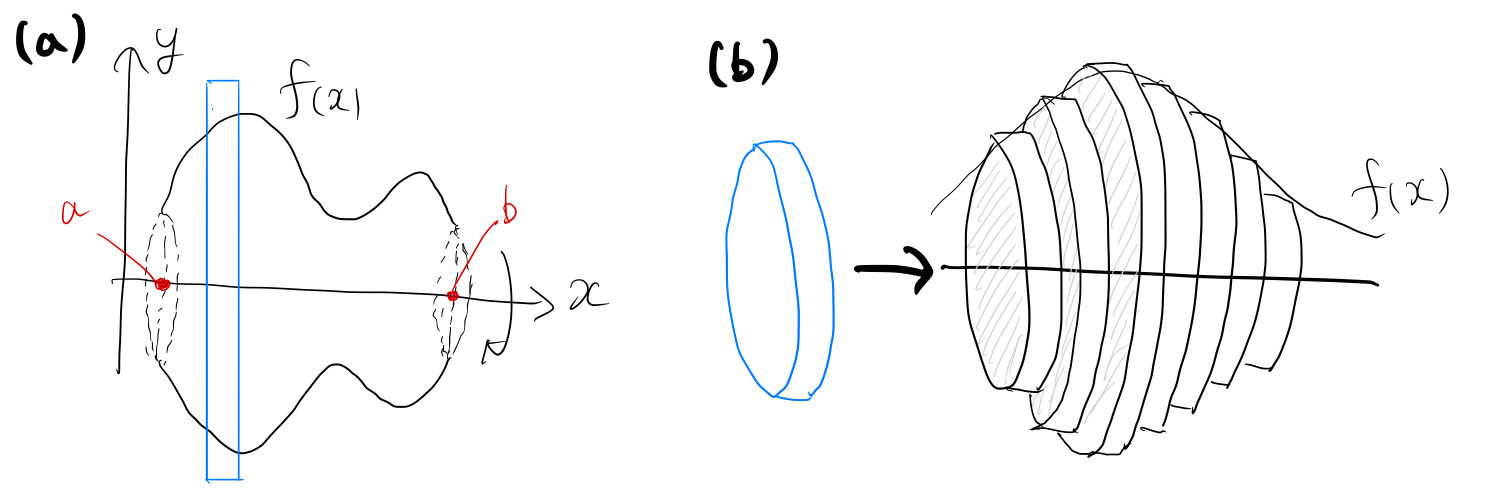
表面積の公式 球- 円錐の表面積の公式の例題 問題 円錐の例 半径3 の円を底面として母線が5 の円錐の表面積Sを求めなさい。 解答 円錐の表面積の公式より となります。 スポンサーリンク シェアする ツイート フォローする nabe 関連記事 2次関数の決定(頂点の座標から)の解法ポイント:二次関数回転体の表面積も求めよう! では次,曲線をx 軸やy 軸のまわりに回転してできる回転体の曲面の表 面積を求める公式についても解説しておこう。 (Ⅰ) について,微小区間x, +Δ における 微小な曲面の表面積 ΔS は,図12 より

空間図形 角柱 角錐 すい 円柱 円錐の体積の求め方 中学数学 定期テスト対策サイト
円錐の表面積を一発で計算する公式 の順で のび校長 小中学生対象完全個別指導塾の校長(経営者兼専任講師) 開校5年半で、新潟県内トップ私立高校合格者を輩出。 年評定平均:中学時代37→高校進学後49、48の塾生を輩出。 サポートした不登校の卒塾生、大学へ進学。 当ブログ、に 球の表面積と体積を求める公式を紹介します。 シンプルに 球の表面積 球の体積 の2種類の公式だけです。とても重要なのでしっかり覚えておきましょう。 小学生の学習や中学受験・試験の対策のために、これだけは"やっとけ"という学習の要点をまとめました。 Yattoke!中学1年生 中学校数学 角錐・円錐の体積と表面積の公式 管理人 2月 5, 19 / 2月 15, 19 中学1年生で習う空間図形には、様々な立体の体積
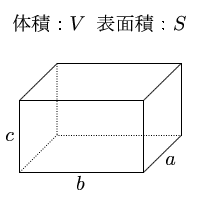
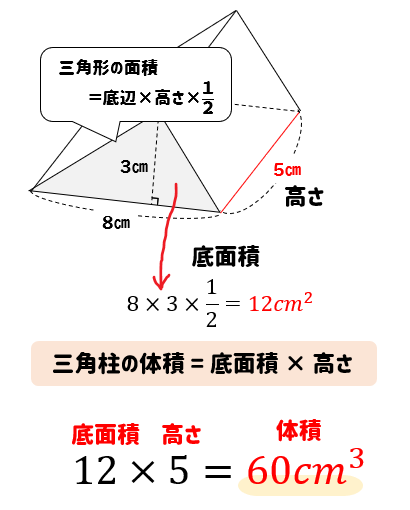
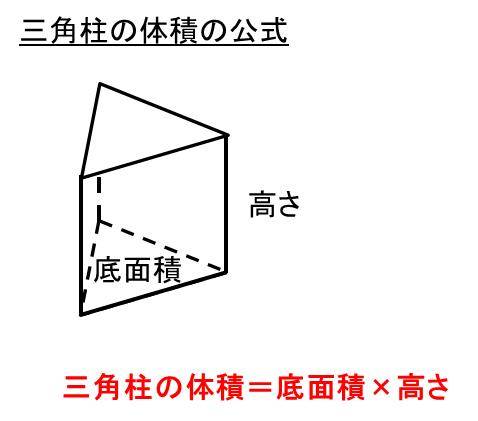
表面積は公式がない場合が多いので『展開図』です。 ※ 展開図が書けない球は後で説明します。 問題2-(3)次の円柱の表面積と体積を求めなさい。 これも柱体なので(1)(2)と同じです。 展開したとき側面が長方形だと覚えておけば、展開図は楽に書けます。 図の赤い 円の周の長さと、長方形の 公式一覧立体の体積・表面積の求め方(円柱・三角柱・円錐・三角錐・球) 体積の公式は何種類もあってわけわからなくなってしまう子が多いです。 ですが、仕組みを知ってしまえば無理して覚えずとも解くことができます。 まずはそれぞれ体積を求める 円柱の表面積の求め方公式 円柱の表面積を求めるときには次の公式を使います。 円柱の表面積=底面積×2+ 円柱の側面積 円柱の側面積 =円柱の高さ×底面の円周の長さ なので 円柱の表面積=底面積×2+円柱の高さ×底面の円周の長さ とも書けます。
表面積の公式 球のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu | 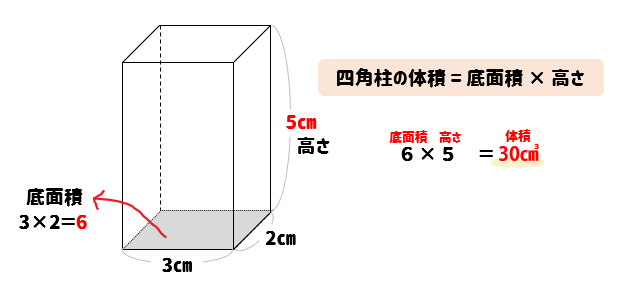 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |
 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu | 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |
中1数学 立体の表面積と体積の求め方と練習問題 Pikuu | 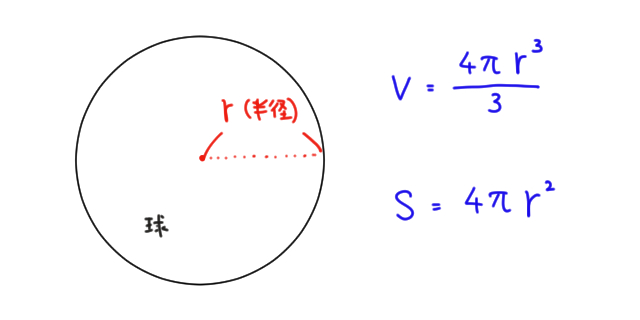 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |
 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |
 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |
 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu | 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |
 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu | 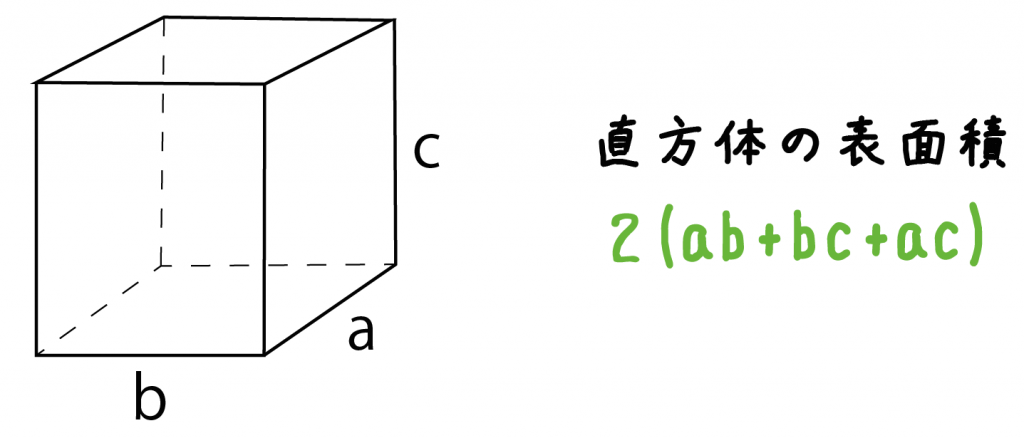 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |
 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu | 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |
 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |
 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |
 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |
 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu | 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |
 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu | 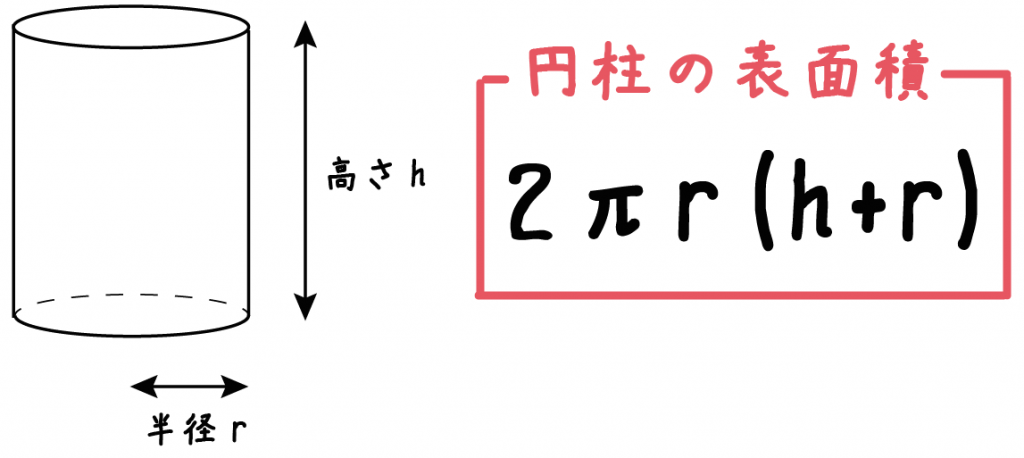 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |
 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |
 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu | 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |
 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu | 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |
 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu | 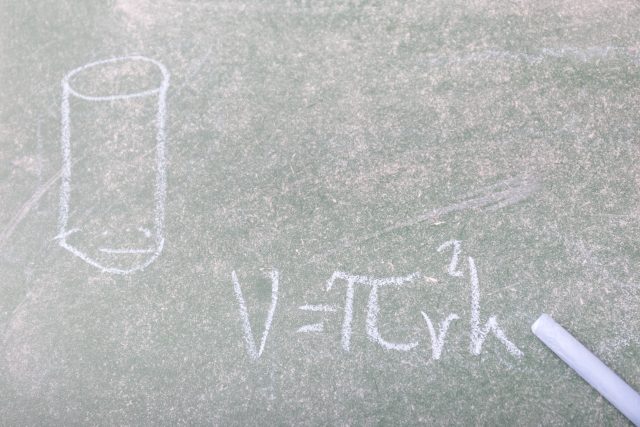 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu | 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |
 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |
中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |
 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu | 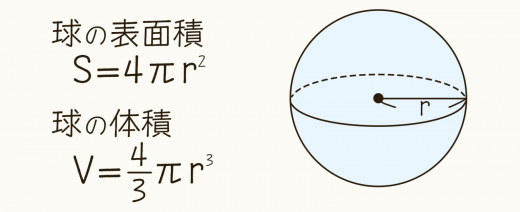 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |
 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |
 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu | 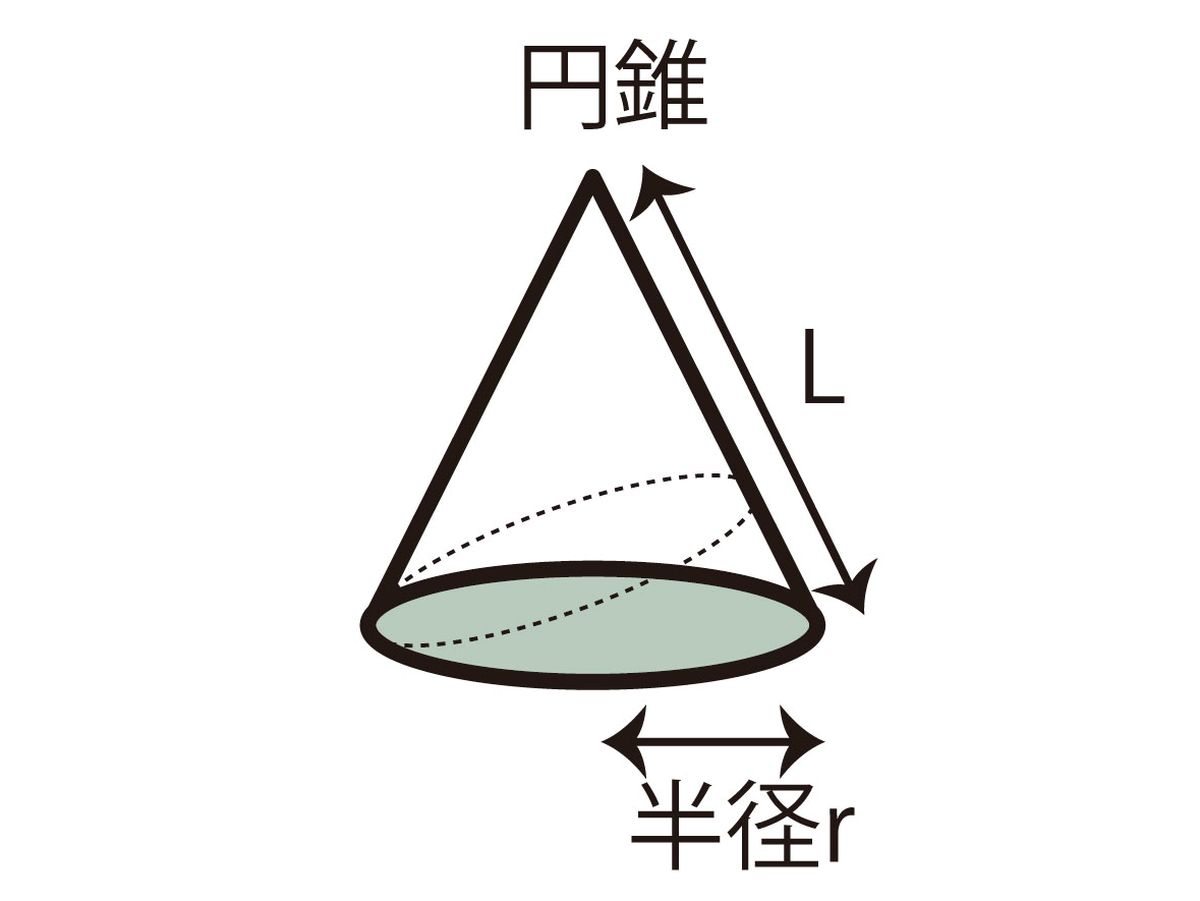 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu | 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |
 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu | 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |
 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu | 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |
 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu | 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |
 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |
 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu | 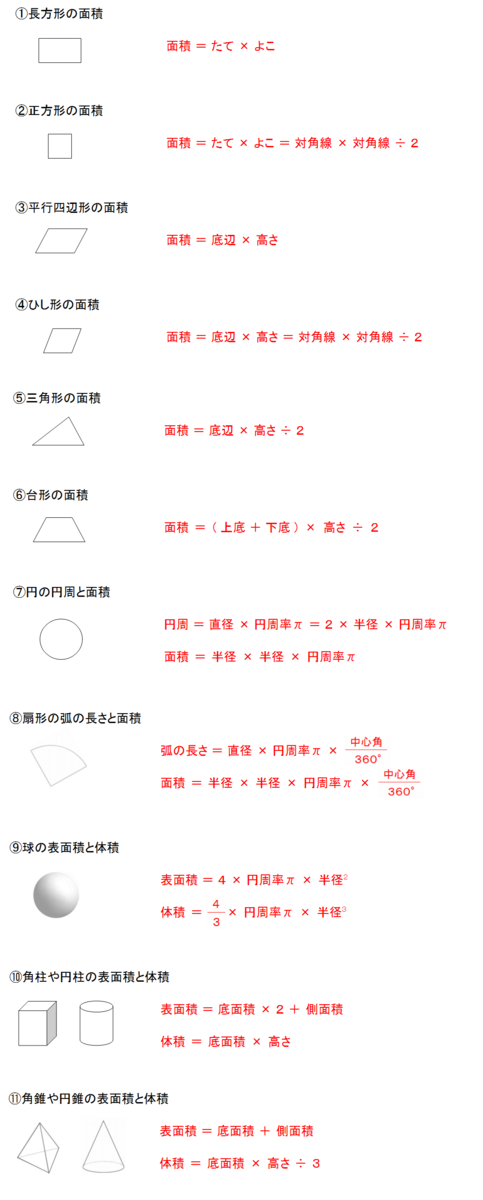 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |
 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |
 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |
 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |
 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu | 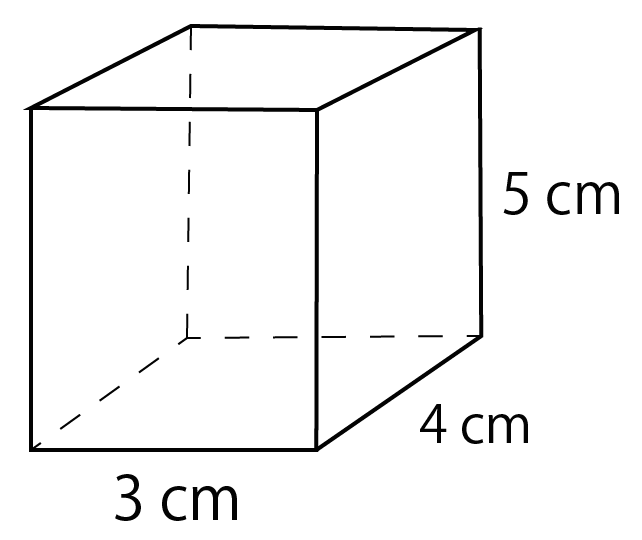 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |
 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |
中1数学 立体の表面積と体積の求め方と練習問題 Pikuu | 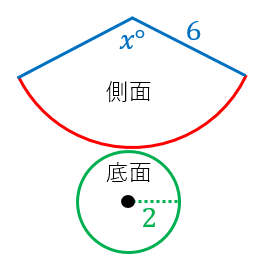 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |
 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu | 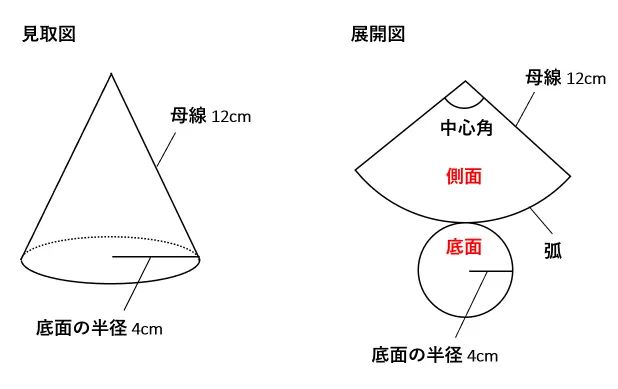 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |
 中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |  中1数学 立体の表面積と体積の求め方と練習問題 Pikuu |
球の表面積の公式はS =4πr² だったので今回は半径5cmなのでrの部分に5を代入してあげると4π × 5² となります 計算をしてあげると50π cm² であるということが分かりました。 それでは次、切り口の面積を求めていきましょう。 今回の半球の表面積を聞かれている場合、こちらの図の 球の表面積の公式は、先ほどの体積の公式から導けます。 証明② 半径 \(t\) の球の表面積を \(S(t)\) と書く。 三次元空間において、原点からの距離が \(t\) 以上 \(t \Delta t\) 以下の間にある部分(球殻)を考える。 \(\Delta t\) が十分小さいとき、この球殻の体積は \((\text{表面
Incoming Term: 表面積の公式, 表面積の公式 球, 表面積の公式 一覧, 表面積の公式 円柱, 表面積の公式 円錐,
コメント
コメントを投稿